Inside X0 and XTR-0

Extropic is proud to publicly reveal our first hardware product: the Experimental Testing & Research Platform 0 (XTR-0).

The currently available version of the XTR-0 platform, which consists of two rectangular daughterboards hosting X-0 chips (top) connected to a trapezoidal motherboard (bottom).

XTR-0 enables the development of ultra-efficient AI algorithms by providing low-latency communication between Extropic chips and a traditional processor. The XTR-0 platform consists of a CPU, an FPGA, and two sockets to receive daughterboards hosting thermodynamic sampling units (TSUs).

The version of XTR-0 that is available today lets users communicate with X0, one of our early test chips, which validated our science and proved that we can make all-transistor Thermodynamic Sampling Units (TSUs).

XTR-0 is straightforwardly upgradable with future Extropic chips, and will soon enable development of novel machine learning algorithms.

TSUs are made of probabilistic circuits

Although modern AI systems are capable of doing amazingly complex things, they are made up of very simple parts. LLMs are nothing more than a pile of simple arithmetic operations, each of which are executed on a processor that is (more or less) a giant array of identical processing cores that do nothing but simple floating point manipulations. Each of these cores is built out of simple logic gates arranged in just the right way to make the math happen.

Instead of wiring together floating point math cores to do arithmetic like today’s AI systems, Extropic’s TSUs wire together a bunch of simple probabilistic circuits to sample from complex probability distributions. This is enabled by the Gibbs sampling algorithm. To learn about how we use Gibbs sampling in our TSUs, you can check out some of our other writing.

While the logic circuits in today’s computers compute simple deterministic operations, probabilistic circuits sample from simple probability distributions. For example, one of the simplest probabilistic circuits is the pbit, which can be used to sample from a programmable Bernoulli distribution (a distribution that models the flipping of a biased coin). You can also make probabilistic circuits that sample from other distributions, like categorical, Gaussian, and mixtures of Gaussians natively in hardware. Below, you can see an example of what a waveform from a pbit might look like, and how it is discretized into 1's and 0's.

X0 derisked the TSU

Probabilistic circuits are not nearly as technologically mature as deterministic logic circuits, and have yet to be used in anything larger than an academic experiment. The main reason for this is that academic probabilistic circuits generally rely on some exotic component to produce randomness, and therefore cannot be built at scale using a conventional transistor process (like one from Intel or GlobalFoundries).

To produce production-scale TSUs, we first had to figure out how to make reliable probabilistic circuits out of transistors. This took years of effort, as we built models of the physics of transistors and developed new ways of understanding noise.

Several bare X0 dies. Most of the complexity of X0 is hidden beneath the surface of the chip. The silver spots are probe structures that enables testing of the chip and transistor process. The small orange specks visible on the lower half of the chip reveal the locations of some of our probabilistic circuits.

X0 is the chip we designed to test our noise models and probabilistic circuit designs. Our experiments using X0 were successful. We found that our models of noise were largely correct, and that our new probabilistic circuit designs worked. These promising results are the first step towards designing and building a full on TSU.

XTR-0 and beyond

XTR-0 + X0 allows users to use our novel probabilistic circuits to run simple hybrid deterministic-thermodynamic algorithms. X0 is too small for this to be commercially useful, but it represents the first time that probabilistic circuits that were manufactured using an advanced, mainstream, semiconductor process can be used to do any computation at all.

We are shipping a limited number of units to various researchers, tinkerers, and startups. We look forward to seeing what sort of fun demonstrations and algorithms the community of early access users will create.

Future Extropic chip releases will be able to interface with XTR-0, allowing XTR-0 recipients to straightforwardly upgrade from X0 prototype chips to our first production-scale TSU, the Z-1.

Our first TSUs will be able to implement non-trivial machine learning algorithms far more complicated than even our largest simulations today.

XTR-0 is the first way Extropic chips will be integrated with conventional computers. We intend to build more advanced systems around future TSUs that allow them to more easily integrate with conventional AI accelerators like GPUs. This could take the form of something simple like a PCIe card, or could in principle be as complicated as building a single chip that contains both a GPU and a TSU.

Our prototype probabilistic circuits

X0 houses a family of circuits that generate samples from primitive probability distributions. Our future chips will combine millions of these probabilistic circuits to run EBMs efficiently.

The probabilistic circuits on X0 output random continuous-time voltage signals. Repeatedly observing the signals (waiting sufficiently long between observations) allows a user to generate approximately independent samples from the distribution embodied by the circuit. These circuits are used to generate the random output voltage, making them much more energy efficient than their counterparts on deterministic digital computers.

Four X-0 chips glued to a PCB to allow for probing and microscope imaging.

The X0 sampling circuits take voltage signals as inputs that allow the distribution parameters to be programmed. Extropic learns the map from control voltages to the resulting distributional parameters implemented by the circuit at the factory. XTR-0 implements this map so users can work with the device without worrying about low-level implementation details.

This section will discuss a few of the most essential sampling circuits featured on XTR-0. The focus will be on how they work from an input-output perspective in isolation rather than how to use them as part of an algorithm. If a discussion of algorithms and applications is more interesting to you, read our other writing.

The pbit

A core subroutine of many probabilistic algorithms is making randomized yes/no decisions. One makes this kind of decision by flipping an appropriately weighted coin. The pbit is a circuit that electronically performs millions to hundreds of millions of such coin flips per second, using 10,000x less energy than a single floating-point add per flip.

The output of the pbit is a voltage signal that switches randomly between a high level and a low level. The high level represents the logical 1 state (or heads in the coin analogy), and the low level represents the logical 0 state (tails). The weighting of the coin flips produced by the pbit is arbitrarily programmable via a single input voltage. For extreme values of this voltage, the pbit will deterministically produce either a 1 or a 0. The output will become random for intermediate control voltage values, and the pbit will sometimes output 1 and sometimes output 0.

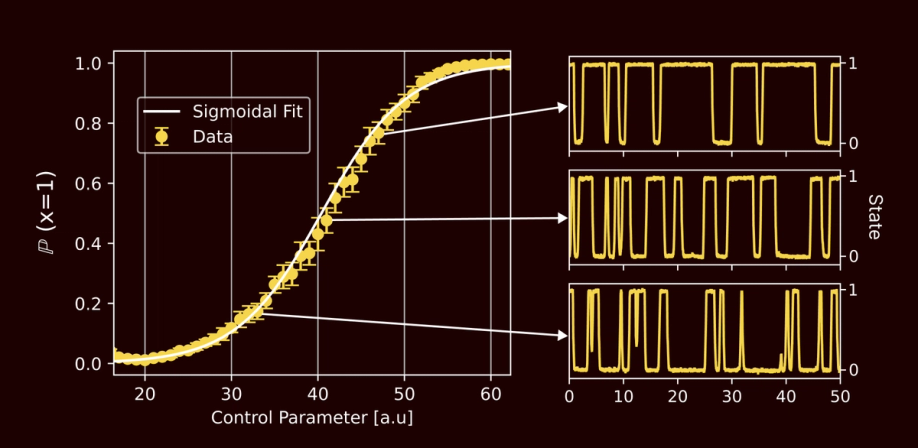
The operating characteristic of the pbit. The bias (probability of finding the pbit in the state 1) is roughly sigmoidal in the control parameter. Modifying the bias parameter has a clear effect on the output waveforms.

Mathematically, the pbit generates samples from a Bernoulli distribution with parameter . Specifically, if we repeatedly observe the output of the Pbit, the output level will be approximately distributed as,

The parameter is controlled by the input voltage, and the functional dependence of on this voltage is roughly sigmoidal. The image above shows the effect of the bias parameter on the wandering output voltages.

To build a fast probabilistic computer, you need sampling circuits with short memories of their prior states. The length of this memory is called the relaxation time of the circuit, and it quantifies how much information is shared between two samples as a function of how much time elapsed between their drawing. In the case of our pbit, we quantify the relaxation time using the normalized autocorrelation function,

In our case, is approximately exponential in with rate ,

For this example, . depends strongly on the specifics of the pbit circuit design/implementation and can vary from to given the fabrication process used for X0.

The pdit

Another standard subroutine in probabilistic algorithms is randomly choosing from one of options. The pdit is a circuit that implements a categorical random variable by acting as an electronic source of loaded dice rolls and is a natural generalization of the pbit. Such -category random variables are called categorical random variables, and they are key components for classifiers or token outputs of language models, amongst others.

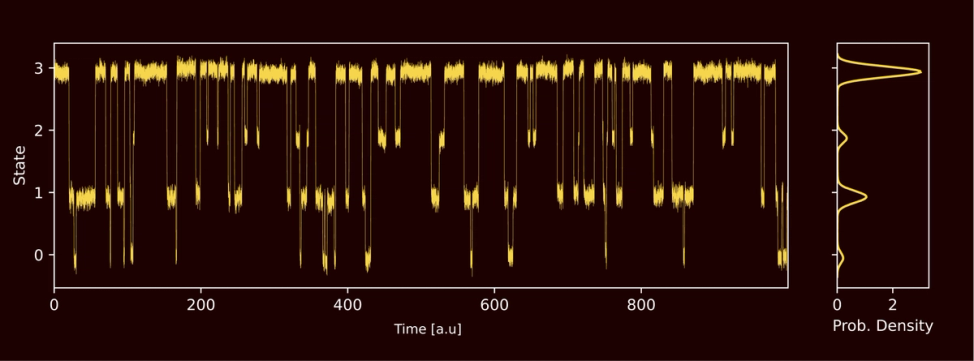
An example of the raw signal generated by a 4-level pdit. The signal rapidly jumps between one of four well-defined discrete levels. A user can program the probability of the signal being in any particular state at a given time by varying 3 independent control parameters.

Like the pbit, the output of the pdit is a voltage signal that wanders between discrete levels. Each discrete level represents a category, and repeatedly observing the pdit signal level constitutes sampling from a -state categorical distribution,

The figure above shows an example output signal from a pdit.

Due to the normalization constraint imposed by , a -state pdit has independent control parameters that users can use to program it to sample from an arbitrary categorical distribution. Like the pbit, input voltages implement these control parameters.

The pmode

Whereas the pbit and pdit sample from discrete distributions, the pmode generates samples from a continuous-valued Gaussian distribution. The utility of the pmode is twofold. Firstly, Gaussian sampling is ubiquitous in probabilistic algorithms (e.g. diffusion models), meaning the pmode is a useful primitive. Secondly, a reliable source of Gaussian noise is beneficial as a building block of more complex sampling circuitry.

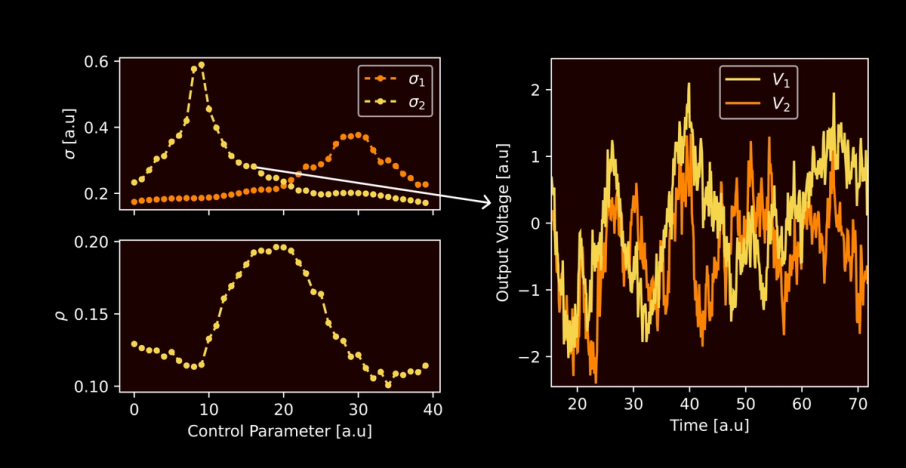
The covariance matrix of a particular 2D PMode as a function of the single control parameter. Increasing the control parameter’s value changes the covariance matrix. When the covariance matrix is tuned to a point with large \rho, the correlations are obvious just from looking at the output voltage timeseries.

Gaussian sampling corresponds to generating samples from the distribution,

where is the mean vector and is the covariance matrix. The pmodes on X0 output a voltage signal that is distributed according to the above equation with programmable .

XTR-0 exposes a 1D pmode and a 2D pmode, both with programmable covariance matrices. Both circuits expose a single control parameter. In the case of the 1D pmode, this parameter controls the standard deviation of the output signal, allowing for control between high and low bounds. For the 2D pmode, the parameter controls the degree of correlation between the two output voltages.

The 2D pmode generates programmably correlated noise. The covariance matrix of a 2D Gaussian distribution is a 2D symmetric matrix. The diagonal elements are the variances of the two output voltage signals and ,

The figure above shows how users can vary a single control parameter to change . For a large value of , the correlations are visually obvious in the output signals. This correlation manifests as a "tilted" Gaussian distribution with a principal axis rotated somewhere between horizontal and vertical.

The pMoG

A pMoG generates data from a mixture of gaussians, also known as a gaussian mixture model (GMM). GMMs are commonly used to represent continuous-valued data that is clustered into distinct groups. XTR-0 features probabilistic primitives that efficiently generate samples from simple programmable GMMs. Gaussian mixtures are richer primitives that have all sorts of applications themselves, from clustering data to Gaussian splatting for 3D rendering.

Programming a 2-mode PMoG. In (a), the mean parameter for one of the modes is swept between two extremes while the other is held constant. In (b), the bias parameter is varied to change the weight put on one mode vs the other.

The output signal from the GMM circuits is similar to the pdit in that it jumps rapidly between several discrete voltage levels. However, in the case of the GMM, both the position of each level and the spread of the signal within a level are programmable. To be precise, a GMM has the distribution,

where each is a Gaussian distribution. The bias paramters set the relative weight of each "mode" of the GMM.

The GMM sampling circuits on XTR0 feature a rich set of control parameters that allow users to control , , and within some bounds.