TSU 101 An Entirely New Type of Computing Hardware

Extropic is building an entirely new type of computing hardware that is designed from the ground up to be incredibly energy efficient at running generative AI models. We call our new type of hardware the thermodynamic sampling unit, or TSU.

A TSU is a type of probabilistic computer that is programmed to sample from probability distributions. The inputs to a TSU are a set of parameters that define the shape of some probability distribution, and the outputs are samples from the defined distribution.

While designs for things like TSUs have existed in academia for decades, Extropic is the first to design a scalable TSU that can be built using standard semiconductor processes.

Generative AI is Sampling

All generative AI algorithms are essentially procedures for sampling from probability distributions. Training a generative AI model corresponds to inferring the probability distribution that underlies some training data, and running inference corresponds to generating samples from the learned distribution. Because TSUs sample, they can run generative AI algorithms natively.

Practitioners may object that modern generative AI algorithms are designed to do as little sampling as possible. This is because existing algorithms have been designed to run well on GPUs, which are really bad at sampling and really good at matrix multiplication.

Generative AI algorithms are well-suited to GPUs because of a decade of co-evolution, not because of intelligent design. GPUs were discovered to be very good at running neural networks over a decade ago. Ever since, machine learning algorithm development has focused on algorithms that run well on GPU-like architectures, and hardware designers have focused on improving GPU-like architectures. The current LLM paradigm is the result of this feedback loop.

Our bet at Extropic is that much more energy efficient AI systems will evolve as people learn how to both build better TSUs and make algorithms that leverage their capabilities more effectively.

How TSUs work

Our TSUs are networks of probabilistic circuits that sample from simple probability distributions. Combining many of these probabilistic circuits together using only local communication allows us to sample from much more complex probability distributions that are useful for generative AI.

To understand how a TSU works, you first have to understand what we mean by a probabilistic circuit, how we can combine these probabilistic circuits into sampling units, and how we can use those sampling units to run generative AI workloads.

We’ll start by examining a simple probabilistic circuit: the pbit.

The Pbit

A pbit is programmed with a probability, and then produces 1 with that probability and produces a 0 otherwise. In other words, a pbit is a programmable analog hardware implementation of a Bernoulli distribution. We program pbits by changing a control voltage, which changes the probability that the pbit will be found in the 1 state at any given time.

To learn more about our ultra-energy-efficient probabilistic circuits, you can read our post about our hardware prototype.

To take a sample, we simply read the output voltage of the pbit. Because the output voltage varies over time, if we wait long enough between samples, we will get new independent samples from the target distribution.

Composing Pbits

Probabilistic circuits like pbits are useful because many of them can be combined to sample from complex probability distributions using an algorithm called Gibbs sampling.

This section will give a high level overview of how Gibbs sampling works in the context of our thermodynamic sampling units. If you are interested in a rigorous explanation of Gibbs sampling, we recommend reading Kevin Murphy's textbook.

We will start with a small example.

Suppose we had a probability distribution defined over two variables and , each of which can possibly take on a value of or . This means there are four states: either both minus, left minus, right minus, or no minuses. Our probability distribution will have four probabilities, one for each of these states.

To represent the probability distribution, we need some way to express those probabilities. We can choose to express our probabilities as an Energy-Based Model (EBM), by setting an “energy” value for each state using an energy function, which is written as .

Because probabilities are proportional to , we can see that the higher the energy value for a state, the less likely that state is.

The shape of the probability distribution can be controlled by varying the parameters of the energy function. In the case of our example, we have access to the bias parameters b0 and b1, along with the coupling parameter w. Large positive bias parameters encourage each variable to be +1 more often than -1, and large positive coupling parameters encourage the two variables to take the same value (since both of these things lead to smaller energy values).

We have a negative sign to make higher weights make it more likely that nodes are positive, which matches our intuitions. Then, inside the negative, increasing increases the probability that , increasing increases the probability that , and increasing w increases the probability that and are in the same state.

This EBM represents a graph with two nodes. Each variable and bias lives on a node, and the two nodes are connected by an edge which carries the interaction weight .

This graphical interpretation makes it clear that our EBM is a very simple example of a probabilistic graphical model (PGM). PGMs provide a useful lens for working with complex sampling problems, but that lens is not needed for this simple case with just two nodes and one edge.

While it is easy to say that the probabilities are proportional to the energy function, it is much harder to compute the actual probabilities. The probabilities need to be normalized, such that the probabilities of each possible state sum to one. We can define a constant, , such that dividing each exponentiated energy by gives us the sum that we want.

However, figuring out the correct value of is computationally expensive. We have to actually compute the energy function for every possible input, and then sum them together. In this case, we would have to evaluate the energy function 4 times for each of the pairs .

Four is a reasonable number of times to evaluate the energy function, but the problem becomes completely intractable as we start getting into the high dimensional distributions that we need for machine learning. If we had a graph with  nodes that each could be or , then computing the value of would require evaluating the energy function times.

Fortunately, Gibbs sampling allows us to draw samples from an EBM without having to compute the value of .

For the above example, running Gibbs sampling corresponds to running the following set of steps:

1. Initialize two bits to anything, say and
2. Compute the bias parameter
3. Update by sampling from a pbit that produces 1 with probability (where is the typical sigmoid/logistic function)
4. Compute the bias parameter
5. Update by sampling from a pbit that produces 1 with probability
6. Repeat steps 2-5 as many times as you want

That procedure is depicted in the animation below.

By running this procedure, we can draw samples from without ever computing the normalizing constant associated with the distribution. If you’re interested, you can read more about how the Gibbs sampling procedure lets us sample from our probability distribution in a textbook.

Gibbs sampling works on much larger examples, too.

Scaling Up

We can expand our model from above to have 16 binary variables, and find a Gibbs sampling procedure that will let us sample from it without computing the normalization constant.

Our 16 variable EBM will have the energy function,

Each node has a bias parameter . The set E contains all of the pairs of variables that interact with each other, with the interaction weight between node and node given by . is an overall “temperature” parameter that scales the strength of all of the weights and biases.

Now that we have sixteen nodes, we can create probability distributions with more complex states. For example, we could set all negative weights between two columns, and all positive weights otherwise, to cause the graph to be likely to have all in one half, and all in the other half. Or we could set every edge weight to be strongly negative, to create a checkerboard type pattern, where probability of a state is higher when there are more neighboring nodes with opposite values. The visualization below shows Gibbs sampling happening over the sixteen nodes.

In general, the Gibbs sampling update for a given node corresponds to sampling from the probability distribution of that node conditioned on each of its neighbors in the graph. As a result, the Gibbs sampling update for each node can be computed by taking the states of the neighboring nodes (ignoring the rest of the graph), using them to compute the parameters of some distribution, and then drawing a sample from that distribution.

Because our graph is bipartite, we can update half of the nodes in parallel, and then update the other half in parallel. As long as the graph stays bipartite, we can increase the size of the grid arbitrarily without increasing the duration of each Gibbs sampling iteration. This is called block Gibbs sampling.

The choice of the edges defined by E fixes the shape of the connection graph. For example, we could choose a set of edges that implements a grid graph, where each node is connected to its von Neumann neighbors. That’s what we did in the visualization above. But in general, a node can be connected to any node from the opposite color in the bipartite coloring.

Gibbs sampling on our 16 node grid is very similar to Gibbs sampling on the 2 node example, with two modifications:

1. The bias parameter for each node is computed using a sum over all of the neighboring node states,
2. Instead of updating one node at a time, we can update blocks of nodes in parallel. In this case, any two nodes that would be the same color on a checkerboard will be updated simultaneously.

With block Gibbs sampling, we can draw samples from an energy-based model by performing a series of simple iterative steps. Now that we have transformed a very hard problem into something much easier, we can turn to building computer hardware to run Gibbs sampling.

Gibbs Sampling in Hardware

We are building a hardware accelerator for PGM Gibbs sampling by directly mapping the math described above onto a chip.

Each node in the PGM gets mapped directly to a hardware sampling cell, and each edge gets mapped to a wire that connects two sampling cells.

Each hardware cell implements the Gibbs sampling update rule for the corresponding node. When performing an update, each cell first receives information about the neighboring variable states over the wires that connect it to other cells. Next, the cell uses this information to compute the parameters of the update distribution. Then, the cell biases a probabilistic circuit according to the parameter values to sample the update. Finally, this updated state is saved to a memory register to allow the state to be communicated to other sampling cells.

In the binary case we considered earlier, a hardware sampling cell design becomes particularly simple (at least in theory). By encoding the variable states into voltages, we can use a programmable resistor network to produce an output voltage that represents . The output voltage of this resistor network can be used to bias a pbit and sample the state update.

But this concept is not limited to binary variables: it is straightforward to extend this idea from the binary case to PGMs over general -category discrete variables with interactions between two or more variables.

Now that we have the hardware, we need to figure out how to use the hardware for generative AI.

Using TSUs for Generative AI

To use a TSU for generative AI, we have to shape an EBMs energy function to match the distribution that underlies some real-world data. That is, we need to find parameters for the energy function that assign low energy to things that look like the training data, and high energy to things that are very different from the training data.

There are many mathematically rigorous ways to accomplish this. In fact, the 2024 Nobel Prize in physics went to Hinton and Hopfield for doing exactly that.

However, trying to directly fit an EBM to the distribution of complicated training data, like all of the text on the internet, is fundamentally a really bad idea.

Real world data is strongly multi-modal, which means that the data is concentrated into clumps that are separated by large regions that are void of data. For example, there are a lot of pictures of dogs on the internet, and also a lot of pictures of airplanes, but very few pictures of dog-airplane hybrids.

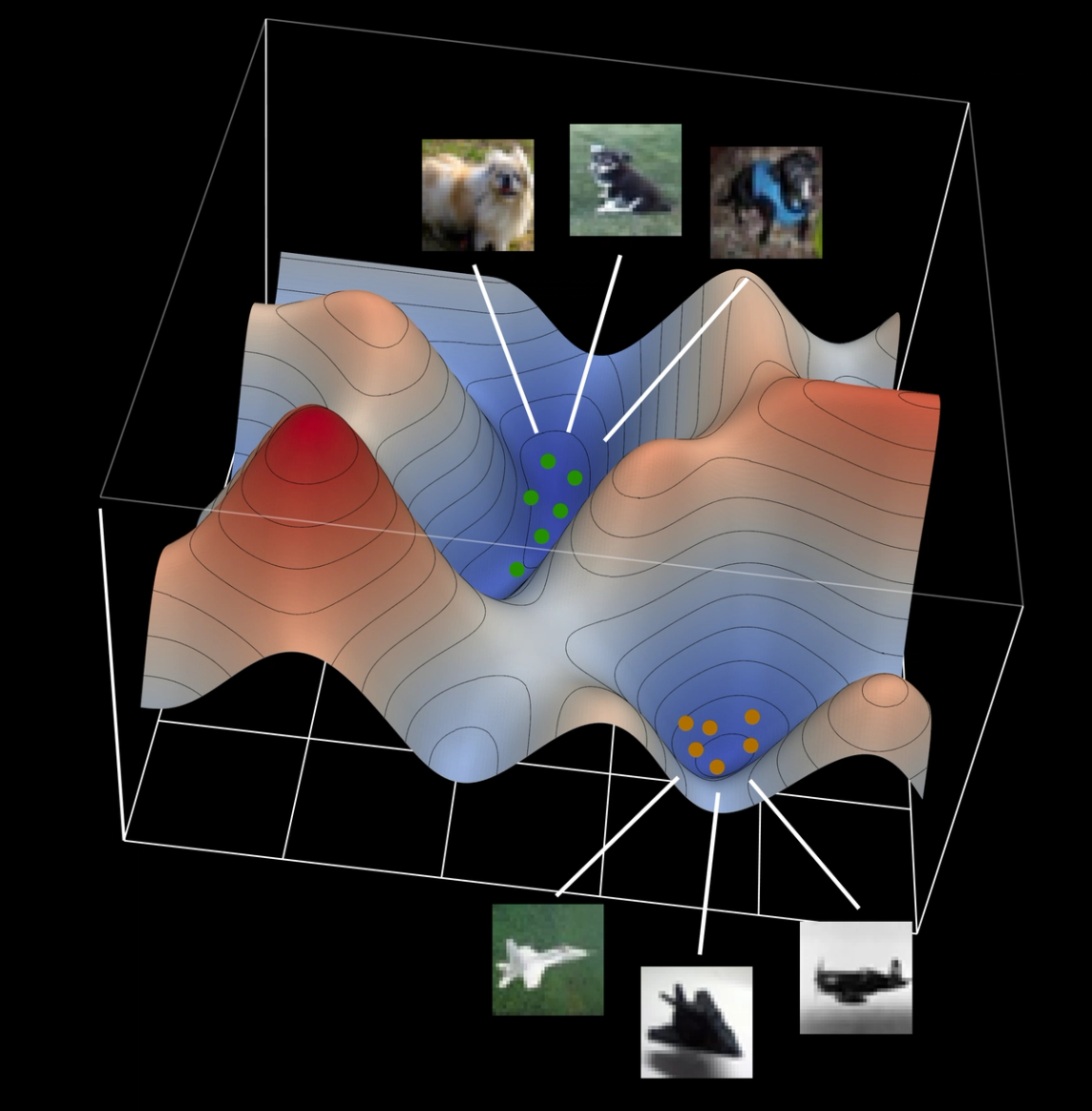
A strongly multi-modal energy landscape. Sampling algorithms have trouble moving between valleys separated by tall mountains, such as the high-energy mountains between the valley with dogs and the valley with airplanes.

Multi-modality is a huge issue for iterative sampling algorithms like Gibbs sampling. Multi-modality traps Gibbs sampling in local minima, which prevents them from actually sampling from the desired distribution. Because iterative sampling algorithms must only very rarely visit states that have high energy, they take an amount of time that is exponential in the height of an energy barrier to cross it.

EBMs fit to real-world datasets are littered with peaks and valleys that can trap samplers. This causes problems in both training and inference.

Previous work on applying TSU-like hardware to machine learning was focused on this direct fitting procedure, which severely limited the efficiency of the overall system.

We realized that to efficiently use a TSU for machine learning, we would have to find a better way to do things.

To find a better way to use TSUs, we looked to the extremely popular denoising diffusion models.

Instead of trying to learn the shape of the data distribution directly in one step, diffusion models learn a many-step procedure that gradually builds up complexity over time. To be more precise, the “forward process” of a diffusion model consists of a series of steps in which data is gradually mixed with noise, such that the output of the forward process is pure noise. Training a denoising model consists of learning a series of models that “undo” the addition of the noise (in a probabilistic sense). With trained denoising models for each step in hand, they can be chained to form a process that converts pure noise back into something that looks like the training data.

The key reason for the success of diffusion models is that each denoising step can be made simpler by increasing the number of steps in the forward process. In fact, if we use an infinite number of steps in the forward process[0], the reverse process becomes so simple that it can be implemented on deterministic hardware like a GPU.

Our key insight is that we can use TSUs to run a denoising model with an non-infinite number of steps[0]. More specifically, for a given problem, we choose a number of steps to use in the forward process so that the distribution of the reverse process is much more complicated than what you would get in the "infinite step” limit but not so complicated that it takes an excessive amount of time to sample.

We call this type of model, which uses EBMs to reverse a denoising process, a Denoising Thermodynamic Model (DTM).

In practice, running inference on a DTM corresponds to running a sequence of sampling programs on TSUs, where the output of one sampling task is fed into the next on as an input (by clamping some of the cells to the output value).

The animation below shows what this looks like at a very granular level for the small TSU and simple generative modeling benchmark that we tested in our paper. Amazingly, we were able to get a grid of only 70x70 sampling cells with local connectivity to generate new low-resolution greyscale images of clothing items from Fashion MNIST. All of the output images that you see were produced by simulations of a 70x70 subsection of our next chip.

We developed a model of our TSU architecture and used it to estimate how much energy it would take to run the denoising process shown in the above animation.

What we found is that DTMs running on TSUs can be about 10,000x more energy efficient than standard image generation algorithms on GPUs.

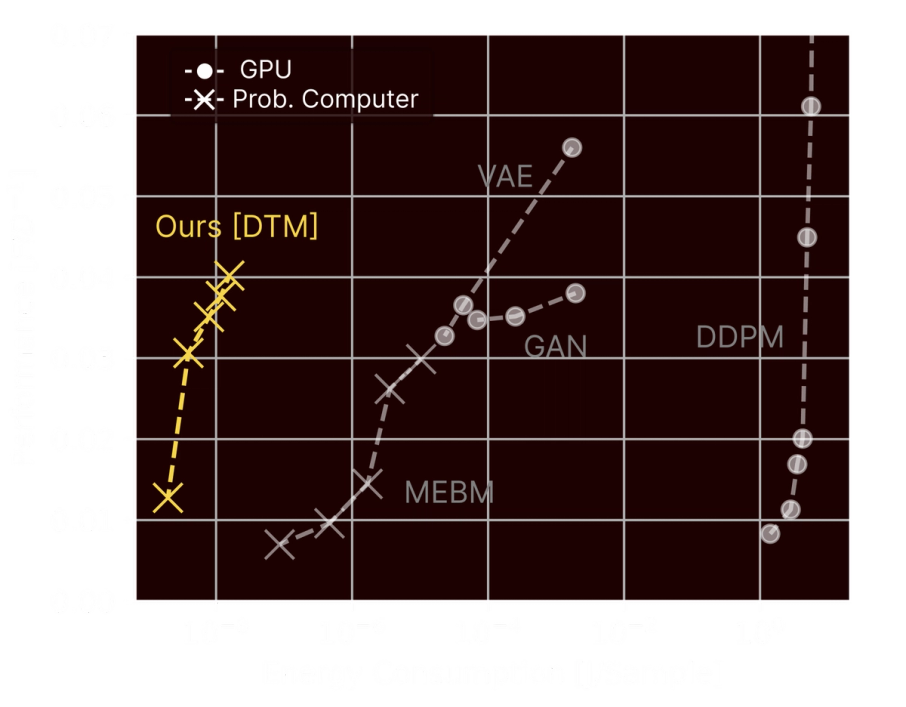
In our paper, we showed that simulations of small sections of our first production-scale TSUs could run small-scale generative AI benchmarks using far less energy than GPUs.

These results are really exciting because they demonstrated that DTMs running on TSUs could be a much more efficient machine learning primitive than matrix multiplications running on GPUs.

The next challenge is to figure out how to combine these primitives in a way that allows for capabilities to be scaled up to something comparable to today’s LLMs.

To do this, we will need to build very large TSUs, and invent new algorithms that can consume an arbitrary amount of probabilistic computing resources.

The Z1 TSU

Our next chip, the Z1 TSU, will have hundreds of thousands of sampling cells.

Because TSUs are really low power, it’s easy enough to imagine large systems involving hundreds or thousands of chips within the footprint of something like an iPhone. Such a system, running in your pocket off a battery, could run models many orders of magnitude more complicated than the simple one discussed in the previous section.

Additionally, Z1 will speed up algorithm development, because using GPUs to simulate TSUs is much slower than running TSUs themselves. As we get better hardware, we will also be able to develop better algorithms to leverage our hardware.

We are working on algorithms internally, and we have also published a Python library, thrml, to allow people to run simulations of both Z1 and other future TSU architectures that Extropic may make.

Because the hardware and the algorithms have to coevolve, we expect to see both algorithmic progress for the Z1 architecture, as well as progress in algorithms that won’t run on Z1 that will inspire Extropic to produce new hardware that can run those algorithms effectively.

A Sample of the Future

We have a clear idea of how to use TSUs to perform generative AI tasks and we are also optimistic that the future will see TSUs used to help accelerate all kinds of probabilistic computing. Similarly to how GPUs were invented to solve the problem of computing graphics for video games, but ended up being used for all kinds of workloads, we think that TSUs will eventually be used to do all probabilistic computing. And, similarly to how some previously non-vectorized algorithms have been replaced with vectorized algorithms to take advantage of the computational primitives provided by GPUs, we think that some deterministic algorithms will be replaced with probabilistic algorithms that take advantage of the computational primitives provided by TSUs.

If you are interested in what you read here, you should consider joining the team to help scale TSUs or the algorithms that can run on TSUs.

If you are an early-career researcher who is interested in studying the theory and application of TSUs, you should consider applying for a research grant.

If you want to experiment or play around with future TSUs, you can use our our software library, thrml, to develop new thermodynamic algorithms for generative AI, simulate our next chip, or investigate different TSU architectures.